Functions

Functions that form the elements of a perceptual control node (system).

Overview

Each function outputs the result of applying the function logic and may be a scalar or array, depending on the input. The inputs are supplied as links to another function, from where the values are read. Unless the function is a simple case, such as a ‘Constant’.

Parameters are supplied as arguments to the constructor of the class.

All functions include the methods defined by the BaseFunction class.

source

HPCTFUNCTION

 HPCTFUNCTION (value, names=None, module=None, qualname=None, type=None,
               start=1)

Types of control functions in a node.

Functions

BaseFunction

source

BaseFunction

 BaseFunction (name=None, value=None, links=None, new_name=True,
               namespace=None)

Base class of a PCT function. This class is not used directly by developers, but defines the functionality common to all.

source

FunctionFactory

 FunctionFactory ()

Initialize self. See help(type(self)) for accurate signature.

#show_doc(BaseFunction.summary)

#show_doc(BaseFunction.get_config)

Subtract

source

Subtract

 Subtract (value=0, name='subtract', links=None, new_name=True,
           namespace=None, **cargs)

A function that subtracts one value from another. Parameter: None. Links: Two links required to each the values to be subtracted.

source

Proportional

 Proportional (gain=1, value=0, name='proportional', links=None,
               new_name=True, namespace=None, **cargs)

A proportion of the input value as defined by the gain parameter. Parameters: The gain value. Links: One.

source

Variable

 Variable (value=0, name='variable', links=None, new_name=True,
           namespace=None, **cargs)

A function that returns a variable value. Parameter: The variable value. Links: None

source

PassOn

 PassOn (value=0, name='variable', links=None, new_name=True,
         namespace=None, **cargs)

A function that passes on a variable value from a linked function. Parameter: None. Links: One

source

GreaterThan

 GreaterThan (threshold=0, upper=1, lower=0, value=0, name='greaterthan',
              links=None, new_name=True, namespace=None, **cargs)

One of two supplied values is returned if the input is greater than supplied threshold.
Parameters: The threshold and upper and lower value. Links: One

source

Constant

 Constant (value=0, name='constant', new_name=True, namespace=None,
           **cargs)

A function that returns a constant value. Parameter: The constant value. Links: None

source

Step

 Step (upper=None, lower=None, delay=None, period=None, value=0,
       name='step', new_name=True, namespace=None, **cargs)

A function that returns an alternating signal. Parameter: The upper and lower values, and a delay value. Links: None

source

Integration

 Integration (gain=1, slow=2, value=0, name='integration', links=None,
              new_name=True, namespace=None, **cargs)

A leaky integrating function. Equivalent of a exponential smoothing function, of the amplified input. Parameters: The gain and slow values. Links: One.

source

IntegrationDual

 IntegrationDual (gain=1, slow=2, value=0, name='integration', links=None,
                  new_name=True, namespace=None, **cargs)

A leaky integrating function, applying one signal to another. Equivalent of a exponential smoothing function, of the amplified input. Parameters: The gain and slow values. Links: Two.

source

Sigmoid

 Sigmoid (range=2, slope=10, value=0, name='sigmoid', links=None,
          new_name=True, namespace=None, **cargs)

A sigmoid function. Similar to a proportional function, but kept within a limit (+/- half the range). Parameters: The range and slope values. Links: One.

source

WeightedSum

 WeightedSum (weights=[0], value=0, name='weighted_sum', links=None,
              new_name=True, usenumpy=False, namespace=None, **cargs)

A function that combines a set of inputs by multiplying each by a weight and then adding them up. Parameter: The weights array. Links: Links to all the input functions.

source

SmoothWeightedSum

 SmoothWeightedSum (weights=[0], smooth_factor=0.0, value=0,
                    name='smooth_weighted_sum', links=None, new_name=True,
                    usenumpy=False, namespace=None, **cargs)

A function that combines a set of inputs by multiplying each by a weight and then adding them up. And then smooths the result. Parameter: The weights array. Links: Links to all the input functions.

source

IndexedParameter

 IndexedParameter (index=None, value=0, name='indexed_parameter',
                   links=None, new_name=True, namespace=None, **cargs)

A function that returns a parameter from a linked function, indexed by number. Parameter: The index. Links: One.

SigmoidWeightedSum

source

SigmoidWeightedSum

 SigmoidWeightedSum (weights=[0], range=2.0, slope=10.0, value=0,
                     name='sigmoid_weighted_sum', links=None,
                     new_name=True, usenumpy=False, namespace=None,
                     **cargs)

A function that combines a set of inputs by multiplying each by a weight and then adding them up. And then limits the output by squashing with a sigmoid function. Parameter: The weights array. Links: Links to all the input functions.

SigmoidSmoothWeightedSum

source

SigmoidSmoothWeightedSum

 SigmoidSmoothWeightedSum (weights=[0], smooth_factor=0.0, range=2.0,
                           slope=10.0, value=0,
                           name='sigmoid_smooth_weighted_sum', links=None,
                           new_name=True, usenumpy=False, namespace=None,
                           **cargs)

A function that combines a set of inputs by multiplying each by a weight and then adding them up. It then smooths the result and then limits the output by squashing with a sigmoid function. Parameter: The weights array. Links: Links to all the input functions.

source

Derivative

 Derivative (history_length=1, value=0, name='derivative', links=None,
             new_name=True, usenumpy=False, namespace=None, **cargs)

A function that provides the difference to previous values of the input signal. Parameter: The weights array. Links: Links to all the input functions.

source

DerivativeWeightedSum

 DerivativeWeightedSum (weights=[0], history_length=1, value=0,
                        name='derivative_weighted_sum', links=None,
                        new_name=True, usenumpy=False, namespace=None,
                        **cargs)

A function that combines a set of inputs by multiplying each by a weight and then adding them up. And then takes the difference of with a past value. Parameter: The weights array. Links: Links to all the input functions.

Usage

Creating Functions

Standard class constructor. Different ways to create a function with the standard constructor.

prop = Proportional()
print(prop.get_config())
prop = Proportional("myprop", 10)
print(prop.get_config())
prop = Proportional(gain=10)
print(prop.get_config())

{'type': 'Proportional', 'name': 'proportional', 'value': 0, 'links': {}, 'gain': 1}
{'type': 'Proportional', 'name': 'proportional', 'value': 10, 'links': {}, 'gain': 'myprop'}
{'type': 'Proportional', 'name': 'proportional', 'value': 0, 'links': {}, 'gain': 10}

Configuration class constructor. Create the function by passing a configuration structure to the constructor.

prop = Proportional(**{'name': 'myprop', 'value': 5, 'gain': 20})
print(prop.get_config())

{'type': 'Proportional', 'name': 'myprop', 'value': 5, 'links': {}, 'gain': 20}

Configuration class method. Create the function by passing a configuration structure to a class method.

config = {'name': 'myprop', 'value': -0.5, 'gain': 21}
prop = Proportional.from_config(config)
print(prop.get_config())

{'type': 'Proportional', 'name': 'myprop', 'value': -0.5, 'links': {}, 'gain': 21}

prop = Proportional()
print(prop.get_config())
prop1 = Proportional.from_config(prop.get_config())
print(prop1.get_config())
assert prop.get_config() == prop1.get_config()

{'type': 'Proportional', 'name': 'proportional', 'value': 0, 'links': {}, 'gain': 1}
{'type': 'Proportional', 'name': 'proportional', 'value': 0, 'links': {}, 'gain': 1}

An example showing creating a WeightedSum function.

wts=[1,1,1]
ws = WeightedSum(weights=wts)
ns = ws.namespace
ws.add_link(Constant(10, namespace=ns))
ws.add_link(Constant(5, namespace=ns))
ws.add_link(Constant(20, namespace=ns))
assert ws() == 35
config = ws.get_config()

#ws1 = WeightedSum.from_config(config, namespace=ns)
ws1 = WeightedSum.from_config(config, new_name= 'weighted_sum1', namespace=ns)
ws1.get_config()

{'type': 'WeightedSum',
 'name': 'weighted_sum1',
 'value': 35,
 'links': {0: 'constant', 1: 'constant1', 2: 'constant2'},
 'weights': [1, 1, 1]}

scons = Constant(2, name='scons')
sig = Sigmoid()
sig.add_link(scons)
sig()

0.9999092042625952

cons = Constant([2,2], name='cons')
print(cons.output_string()+ "")

[2, 2]

Viewing Functions

View the details of the function with the “summary”, which prints the name, type, parameters, value and links (if any).

prop.summary()

proportional Proportional | gain 1 | 0

As already seen the function details can be seen by retrieving the configuration.

print(prop.get_config())

{'type': 'Proportional', 'name': 'proportional', 'value': 0, 'links': {}, 'gain': 1}

Or you can print the function.

print(prop)

{'namespace': UUID('6d28b227-62e7-11ef-87fe-5c879c15de65'), 'value': 0, 'links': [], 'checklinks': True, 'name': 'proportional', 'decimal_places': 3, 'gain': 1}

Set the decimal places for output display.

print(prop.output_string())
prop.set_decimal_places(2)
print(prop.output_string())

0.000
0.00

You can also view a function graphically as a network of connected nodes.

sub = Subtract(links=[Constant(1, name='cons'), Proportional(10, name='prop')], name='sub')
print(sub.value)
g = sub.graph()
print(g)
sub.draw(node_size=2000)

0
DiGraph with 3 nodes and 2 edges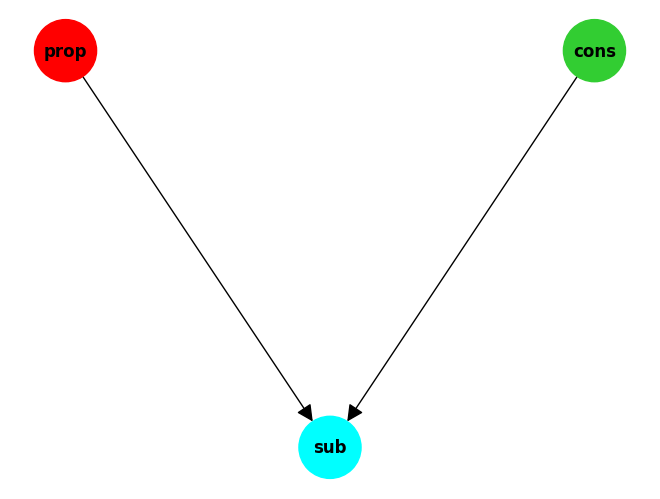

Save and Load

Save a function to file.

import json

print(ws.get_config())
ws.save("ws.json")

{'type': 'WeightedSum', 'name': 'weighted_sum', 'value': 35, 'links': {0: 'constant', 1: 'constant1', 2: 'constant2'}, 'weights': [1, 1, 1]}

Create a function from file.

wss = WeightedSum.load("ws.json", new_name='weighted_sum1', namespace=ns)
print(ws.get_config())
print(wss.get_config())
assert wss.get_config() == {'type': 'WeightedSum', 'name': 'weighted_sum2', 'value': 35, 'links': {0: 'constant', 1: 'constant1', 2: 'constant2'}, 'weights': [1, 1, 1]}

{'type': 'WeightedSum', 'name': 'weighted_sum', 'value': 35, 'links': {0: 'constant', 1: 'constant1', 2: 'constant2'}, 'weights': [1, 1, 1]}
{'type': 'WeightedSum', 'name': 'weighted_sum2', 'value': 35, 'links': {0: 'constant', 1: 'constant1', 2: 'constant2'}, 'weights': [1, 1, 1]}

Setting Links

The next cell shows how a link is added to one function from another. In this case from an Integration function to a Constant function. So, whenever “integrator” runs it will get its input from “cons”.

integrator = Integration(3, 10)
cons = Constant(5)
integrator.add_link(cons)
integrator.summary()

output = integrator()
print(output)
assert output == 1.5

integration Integration | gain 3 slow 10  | 0 | links  constant 
1.5

UniqueNamer.getInstance().clear() # initialises the list of function names
integ = Integration(**{'name': 'myinteg', 'value': 1, 'gain': 20, 'slow': 100})
prop = Proportional(5, name="myprop")
integ.add_link(prop)
print(integ.get_config())
assert integ.get_config() == {'type': 'Integration', 'name': 'myinteg', 'value': 1, 'links': {0: 'myprop'}, 'gain': 20, 'slow': 100}

{'type': 'Integration', 'name': 'myinteg', 'value': 1, 'links': {0: 'myprop'}, 'gain': 20, 'slow': 100}

You can also define the link when you create the function, as in this example with “Proportional”.

const = Constant(1, name='const')
ns = const.namespace
print(const())
pr1 = Proportional(name='pr1', links=const, namespace=ns)
pr1.summary()
assert pr1() == 1

1
pr1 Proportional | gain 1 | 0 | links  const

It can be the name of the linked function.

pr = Proportional(gain=10, name='pr', links='const', namespace=ns)
pr.summary()
assert pr() == 10
print(pr())

pr Proportional | gain 10 | 0 | links  const 
10

Or it can be a list of names.

sub = Subtract(links=[ 'pr', 'const'], namespace=ns)
print(sub.get_config())
print(const())
print(pr())
print(pr())
sub.summary()
print(sub())
assert sub()==9

{'type': 'Subtract', 'name': 'subtract', 'value': 0, 'links': {0: 'pr', 1: 'const'}}
1
10
10
subtract Subtract | 0 | links  pr const 
9

Running a Fucntion

A function can simply be run by calling it, without any parameters. It will use whatever input was set by the links. It returns the result of the function. In this example it will be 5 * 3 / 10, that is, input * gain / slow.

out = sub()
print(out)

A function can be also run in a loop with the run() method and provided the loop count.

integrator = Integration(gain=3, slow=10)
integrator.add_link(sub)
o = integrator.run(steps=10, verbose=True)

2.700 5.130 7.317 9.285 11.057 12.651 14.086 15.377 16.540 17.586

integrator(verbose=True)

18.527

18.527113905569998

output = integrator()
print(output)
#assert output == 1.5
npt.assert_almost_equal(output, 19.374402515013)

19.374402515013

print(integrator.get_config())

{'type': 'Integration', 'name': 'integration', 'value': 19.374402515013, 'links': {0: 'subtract'}, 'gain': 3, 'slow': 10}

An example showing creating and running a sigmoid WeightedSum function.

wts=[0.01,0.01,0.01]
sgws = SigmoidWeightedSum(weights=wts, range=1.0, slope=5.0)
ns = sgws.namespace
sgws.add_link(Constant(10, namespace=ns))
sgws.add_link(Constant(5, namespace=ns))
sgws.add_link(Constant(20, namespace=ns))
sgws.summary()
print(sgws.get_parameters_list())

out = sgws()
print(out)
assert out == 0.3519528019683106

sigmoid_weighted_sum SigmoidWeightedSum | weights [0.01, 0.01, 0.01] range 1.00  slope 5.00 | 0 | links  constant constant1 constant2 
[[0.01, 0.01, 0.01], 1.0, 5.0]
0.3519528019683106

An example showing creating and running a sigmoid smooth WeightedSum function.

wts=[0.01,0.01,0.01]
sgsmws = SigmoidSmoothWeightedSum(weights=wts, smooth_factor=0.9)
ns = sgsmws.namespace
sgsmws.add_link(Constant(10, namespace=ns))
sgsmws.add_link(Constant(5, namespace=ns))
sgsmws.add_link(Constant(20, namespace=ns))
sgsmws.summary()
print(sgsmws.get_parameters_list())
print(sgsmws.get_graph_name())
labels = {}
sgsmws.get_weights_labels_funcdata(labels)
print('wts labels',labels)
for _ in range(5):
    # print(sgsmsm())
    out = sgsmws()
    print(out)

npt.assert_almost_equal(out, 0.34373448930708195)

sigmoid_smooth_weighted_sum SigmoidSmoothWeightedSum | weights [0.01, 0.01, 0.01] smooth 0.90 range 2.00  slope 10.00 | 0 | links  constant constant1 constant2 
[[0.01, 0.01, 0.01], 0.9, 2.0, 10.0]
sigmoid_smooth_weighted_sum
0.90:2.00|10.00
wts labels {('sigmoid_smooth_weighted_sum\n0.90:2.00|10.00', 'constant\n10.00'): '0.01', ('sigmoid_smooth_weighted_sum\n0.90:2.00|10.00', 'constant1\n5.00'): '0.01', ('sigmoid_smooth_weighted_sum\n0.90:2.00|10.00', 'constant2\n20.00'): '0.01'}
0.08727737447415773
0.16473508145615878
0.23277835967904958
0.2921474527779875
0.34373448930708195

An example showing creating and running a smoothed WeightedSum function.

wts=[1.0,1.0,1.0]
wts=[0.01,0.01,0.01]
smws = SmoothWeightedSum(weights=wts, smooth_factor=0.9)
ns = smws.namespace
smws.add_link(Constant(10, namespace=ns))
smws.add_link(Constant(5, namespace=ns))
smws.add_link(Constant(20, namespace=ns))
smws.summary()
print(smws.get_parameters_list())
print(smws.get_graph_name())
for _ in range(5):
    out = smws()
    print(out)

npt.assert_almost_equal(out, 0.1433285)

smooth_weighted_sum SmoothWeightedSum | weights [0.01, 0.01, 0.01] smooth 0.90 | 0 | links  constant constant1 constant2 
[[0.01, 0.01, 0.01], 0.9]
smooth_weighted_sum
0.90
0.034999999999999996
0.0665
0.09485
0.120365
0.1433285

An example showing creating and running a derivative function.

dv = Derivative(history_length=5)
ns = dv.namespace
cons = Constant(10, namespace=ns)
dv.add_link(cons)
dv.summary()
print(dv.get_config())
print(dv.get_parameters_list())
print(dv.get_graph_name())
labels = {}
dv.get_weights_labels(labels)
print(labels)
for i in range(20):
    cons.set_value(i*i)
    out = dv()
    print(out, end=" ")

print()
assert out == -136
print(dv.history)
assert dv.history == [225, 256, 289, 324, 361]

derivative Derivative | history_length 5  | 0 | links  constant 
{'type': 'Derivative', 'name': 'derivative', 'value': 0, 'links': {0: 'constant'}, 'history_length': 5}
[5]
derivative
5.00
{}
0 -1 -4 -9 -16 -24 -32 -40 -48 -56 -64 -72 -80 -88 -96 -104 -112 -120 -128 -136 
[225, 256, 289, 324, 361]

An example showing creating a derivative WeightedSum function.

wts=[0.01,0.01,0.01]
dvws = DerivativeWeightedSum(weights=wts, history_length=5)
ns = dvws.namespace
cons = Constant(10, namespace=ns)
dvws.add_link(cons)

#dvws.add_link(Constant(10, namespace=ns))
dvws.add_link(Constant(5, namespace=ns))
dvws.add_link(Constant(20, namespace=ns))
dvws.summary()
print(dvws.get_config())
print(dvws.get_parameters_list())
print(dvws.get_graph_name())
labels = {}
dvws.get_weights_labels(labels)
print(labels)
for i in range(20):
    cons.set_value(i*i)
    out = dvws()
    print(out, end=" ")

print()
npt.assert_almost_equal(out, -1.3599999999999999)
print(dvws.history)
assert dvws.history == [2.5, 2.81, 3.14, 3.49, 3.86]

derivative_weighted_sum DerivativeWeightedSum | weights [0.01, 0.01, 0.01] history_length 5 | 0 | links  constant constant1 constant2 
{'type': 'DerivativeWeightedSum', 'name': 'derivative_weighted_sum', 'value': 0, 'links': {0: 'constant', 1: 'constant1', 2: 'constant2'}, 'weights': [0.01, 0.01, 0.01], 'history_length': 5}
[[0.01, 0.01, 0.01], 5]
derivative_weighted_sum
5
{('derivative_weighted_sum', 'constant'): '0.01', ('derivative_weighted_sum', 'constant1'): '0.01', ('derivative_weighted_sum', 'constant2'): '0.01'}
0.0 -0.010000000000000009 -0.040000000000000036 -0.09000000000000002 -0.16000000000000003 -0.24 -0.31999999999999995 -0.39999999999999997 -0.4800000000000001 -0.56 -0.64 -0.72 -0.7999999999999998 -0.8799999999999999 -0.96 -1.04 -1.12 -1.2000000000000002 -1.2800000000000002 -1.3599999999999999 
[2.5, 2.81, 3.14, 3.49, 3.86]

wts=[0.01,0.01,0.01]
dvws = DerivativeWeightedSum(weights=wts, history_length=0)
ns = dvws.namespace
cons = Constant(10, namespace=ns)
dvws.add_link(cons)
dvws.add_link(Constant(5, namespace=ns))
dvws.add_link(Constant(20, namespace=ns))
dvws.summary()
print(dvws.get_config())
print(dvws.get_parameters_list())
print(dvws.get_graph_name())
labels = {}
dvws.get_weights_labels(labels)
print(labels)
for i in range(20):
    cons.set_value(i*i)
    out = dvws()
    print(out, end=" ")

print()
npt.assert_almost_equal(out, 3.86)

derivative_weighted_sum DerivativeWeightedSum | weights [0.01, 0.01, 0.01] history_length 0 | 0 | links  constant constant1 constant2 
{'type': 'DerivativeWeightedSum', 'name': 'derivative_weighted_sum', 'value': 0, 'links': {0: 'constant', 1: 'constant1', 2: 'constant2'}, 'weights': [0.01, 0.01, 0.01], 'history_length': 0}
[[0.01, 0.01, 0.01], 0]
derivative_weighted_sum
0
{('derivative_weighted_sum', 'constant'): '0.01', ('derivative_weighted_sum', 'constant1'): '0.01', ('derivative_weighted_sum', 'constant2'): '0.01'}
0.25 0.26 0.29000000000000004 0.34 0.41000000000000003 0.5 0.61 0.74 0.8900000000000001 1.06 1.25 1.46 1.69 1.94 2.21 2.5 2.81 3.14 3.49 3.86

Examples

Configuration

Create a function from the configuration of another.

integrator = Integration(3, 10)
ns=integrator.namespace
cons = Constant(5, namespace=ns)
integrator.add_link(cons)
config = integrator.get_config()
inte = Integration.from_config(config, new_name='integration1', namespace=ns)
print(inte())
target = {'type': 'Integration', 'name': 'integration1', 'value': 1.5, 'links': {0: 'constant'}, 'gain': 3, 'slow': 10}
print(target)
assert inte.get_config() == target

1.5
{'type': 'Integration', 'name': 'integration1', 'value': 1.5, 'links': {0: 'constant'}, 'gain': 3, 'slow': 10}